Funções Periódicas e Funções Trigonométricas
Uma função periódica repete seus valores em intervalos regulares. Se fx+P = f(x) para todo x no domínio, dizemos que P é um período da função. O menor valor positivo de P é chamado de período fundamental.
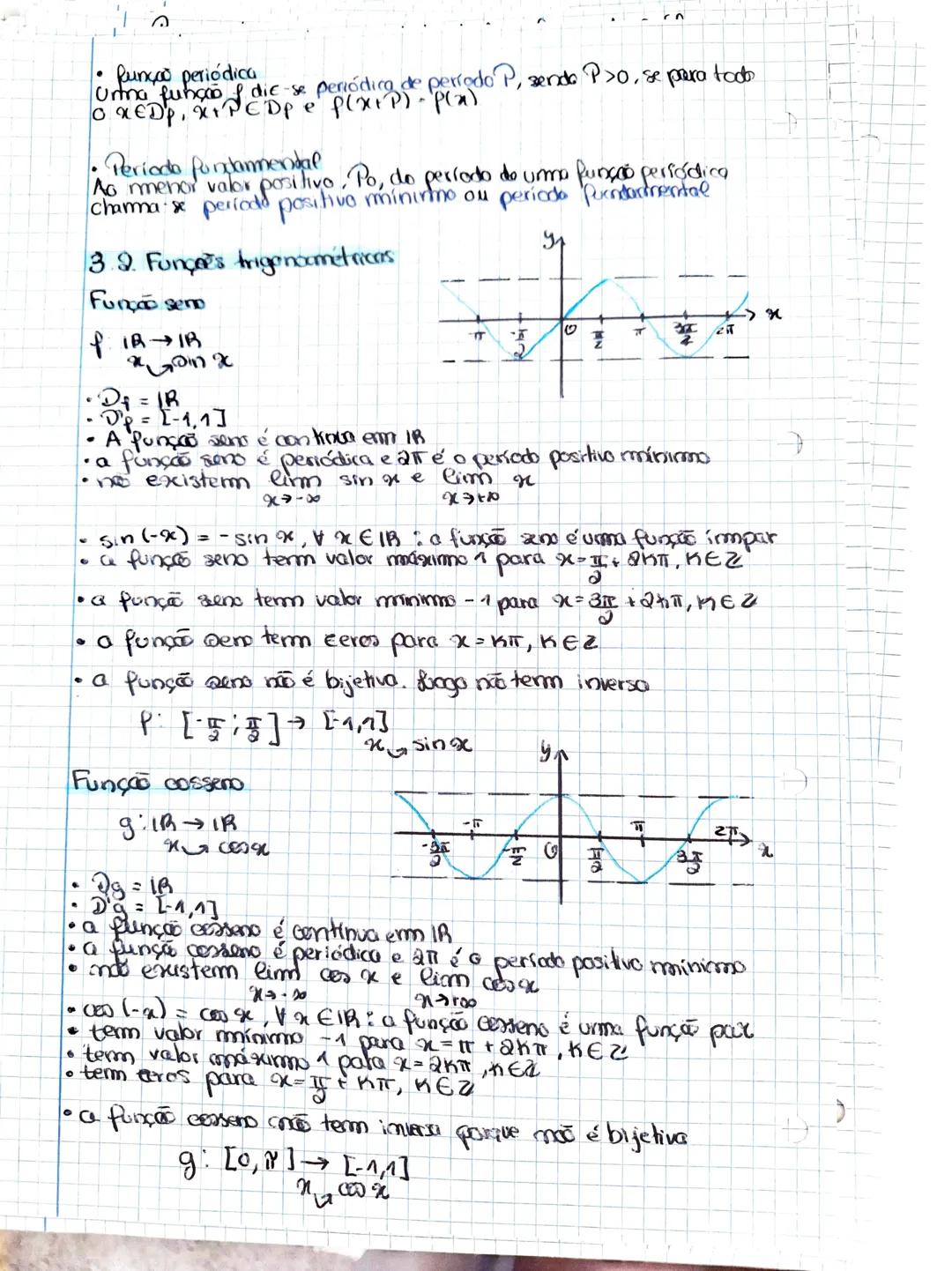
A função seno f(x)=sinx tem as seguintes propriedades:
- Domínio: todos os números reais
- Imagem: [-1, 1]
- É contínua em todo seu domínio
- Tem período fundamental 2π
- É uma função ímpar: sin−x = -sin(x)
A função seno atinge seu valor máximo (1) quando x = π/2 + 2kπ, seu valor mínimo (-1) quando x = 3π/2 + 2kπ, e tem zeros quando x = kπ, para k ∈ Z.
Visualize isto: A função seno produz a familiar "onda senoidal" que oscila entre -1 e 1, completando um ciclo completo a cada 2π unidades.
A função cosseno g(x)=cosx apresenta características semelhantes:
- Domínio: todos os números reais
- Imagem: [-1, 1]
- Período fundamental: 2π
- É uma função par: cos−x = cos(x)
O cosseno atinge seu valor máximo (1) quando x = 2kπ, seu valor mínimo (-1) quando x = π + 2kπ, e tem zeros quando x = π/2 + kπ, para k ∈ Z.
Estas funções são fundamentais para modelar fenômenos cíclicos como ondas sonoras, corrente elétrica alternada e movimentos oscilatórios.