Trigonometria do Triângulo Retângulo

No triângulo retângulo, as razões trigonométricas relacionam os lados com os ângulos. As três principais são:

• seno: relação entre o cateto oposto e a hipotenusa $sen α = cateto oposto/hipotenusa$
• cosseno: relação entre o cateto adjacente e a hipotenusa $cos α = cateto adjacente/hipotenusa$
• tangente: relação entre o cateto oposto e o cateto adjacente $tan α = cateto oposto/cateto adjacente$

Existe uma relação importante entre ângulos complementares: sen (90°-α) = cos α, cos (90°-α) = sen α, e tan (90°-α) = 1/tan α.

💡 A Fórmula Fundamental da Trigonometria $sen²α + cos²α = 1$ é uma das relações mais importantes e será usada frequentemente para resolver problemas trigonométricos.

Fórmulas Trigonométricas e Valores Notáveis

A partir da Fórmula Fundamental $sen²α + cos²α = 1$ podemos derivar outras relações importantes:

• Dividindo tudo por cos²α: sen²α/cos²α + 1 = 1/cos²α → tg²α + 1 = 1/cos²α
• Dividindo tudo por sen²α: 1 + cos²α/sen²α = 1/sen²α → 1 + 1/tg²α = 1/sen²α

Os valores trigonométricos notáveis são essenciais para cálculos rápidos. Memoriza-os:

💡 Estes valores aparecem frequentemente nos problemas. Memorizar esta tabela vai poupar-te muito tempo nos testes!

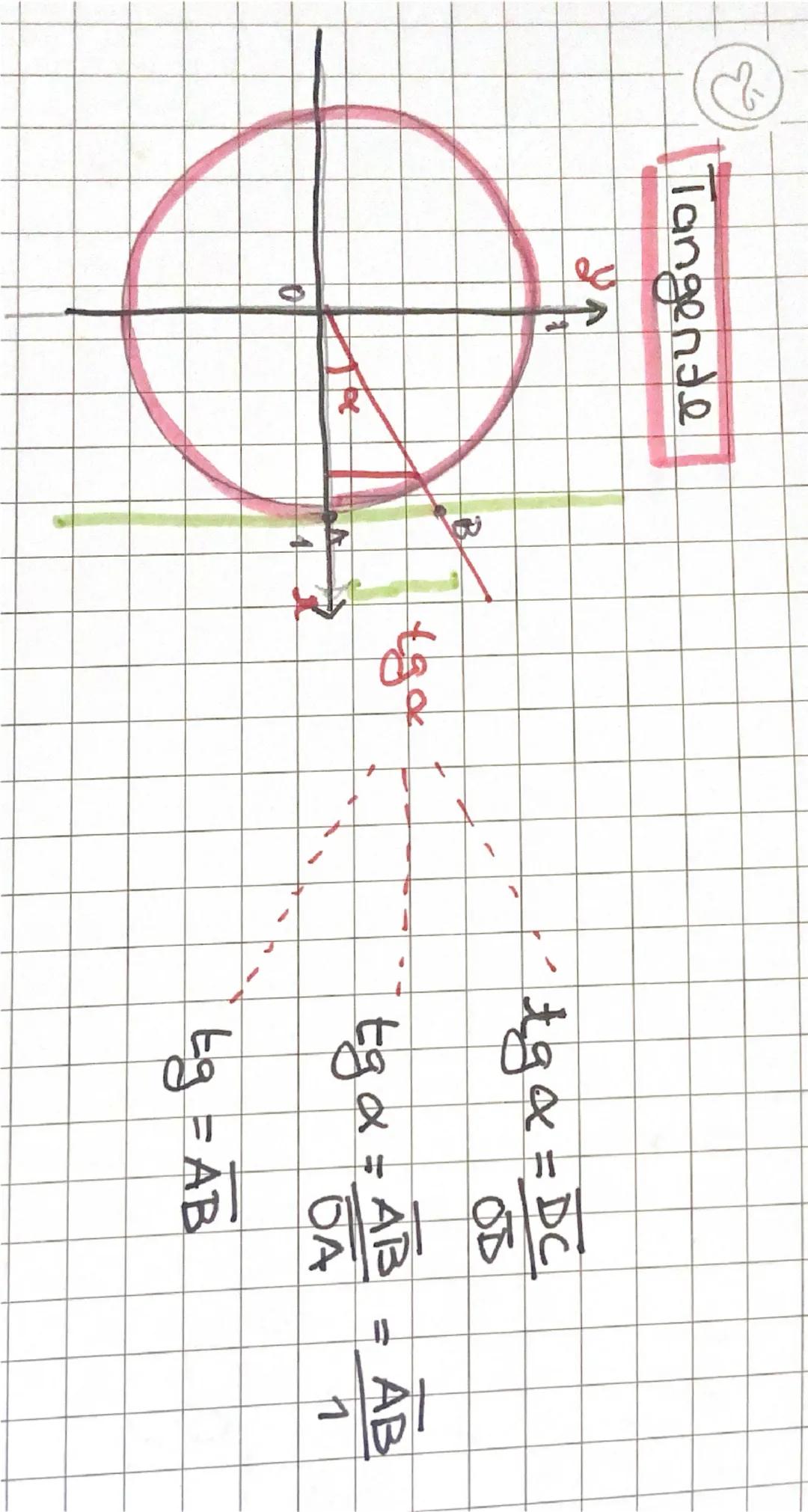
Círculo Trigonométrico

O círculo trigonométrico é uma representação gráfica fundamental com raio igual a 1. Cada ponto no círculo tem coordenadas que correspondem a valores trigonométricos.

Para qualquer ângulo α, o ponto A no círculo tem coordenadas (cos α, sen α). Isto significa que a coordenada x é o cosseno do ângulo e a coordenada y é o seno.

Se tivermos um ângulo maior que 360° (ou 2π), reduzimos ao círculo subtraindo voltas completas. Por exemplo, se α = 405°, calculamos 405° - 360° = 45°, então usamos o ponto A (cos 45°, sen 45°) = (√2/2, √2/2).

💡 O círculo trigonométrico funciona como um "mapa" para todas as funções trigonométricas. Visualizá-lo ajuda a compreender os sinais e comportamentos das funções em diferentes quadrantes.

Seno e Cosseno no Círculo Trigonométrico

A função seno corresponde à coordenada y no círculo trigonométrico, variando entre -1 e 1:

• sen 0 = 0
• sen π/2 = 1
• sen π = 0
• sen 3π/2 = -1

A função cosseno corresponde à coordenada x, também variando entre -1 e 1:

• cos 0 = 1
• cos π/2 = 0
• cos π = -1
• cos 3π/2 = 0

Os sinais destas funções variam conforme o quadrante:

• Seno é positivo no 1º e 2º quadrantes
• Seno é negativo no 3º e 4º quadrantes
• Cosseno é positivo no 1º e 4º quadrantes
• Cosseno é negativo no 2º e 3º quadrantes

💡 Para lembrar facilmente onde cada função é positiva, usa a regra "COSSENO SENO TANGENTE": Com Sorrisos Todos (1º quadrante), Cala-te Sorri Triste (2º quadrante), Chorando Sempre Triste (3º quadrante), Choras Só Tu (4º quadrante).

Tangente

A tangente é definida como a razão entre seno e cosseno: tg α = sen α/cos α.

No círculo trigonométrico, a tangente representa a medida do segmento AB, onde A é o ponto (cos α, sen α) no círculo e B é o ponto onde a reta que passa por A e pela origem intersecta a reta vertical que passa por (1,0).

Como o raio do círculo trigonométrico é 1, temos: tg α = AB/OA = AB/1 = AB

A tangente não está definida quando cos α = 0, o que acontece nos ângulos π/2 + kπ $90° + k180°$.

💡 A tangente é a única das três funções trigonométricas principais que não tem limite superior ou inferior - ela pode variar de -∞ a +∞!

Redução ao Primeiro Quadrante

A redução ao primeiro quadrante é uma técnica essencial para calcular valores trigonométricos em qualquer ângulo, relacionando-os com ângulos no 1º quadrante.

Para ângulos negativos:

• sen(-α) = -sen α (função ímpar)
• cos(-α) = cos α (função par)
• tg(-α) = -tg α (função ímpar)

Para ângulos no 2º quadrante $π/2 até π$:

• sen(π/2 + α) = cos α
• cos(π/2 + α) = -sen α
• tg(π/2 + α) = -1/tg α

Para ângulos no 2º quadrante (outra forma):

• sen(π - α) = sen α
• cos(π - α) = -cos α
• tg(π - α) = -tg α

💡 Quando o ângulo está sobre um dos eixos, lembra que "a palavra muda" - cosseno vira seno e seno vira cosseno. Isto aplica-se aos ângulos π/2 ± α.

Mais Relações de Redução

Para ângulos no 3º quadrante $π até 3π/2$:

• sen(π + α) = -sen α
• cos(π + α) = -cos α
• tg(π + α) = tg α

Para ângulos no 4º quadrante $3π/2 até 2π$:

• sen(3π/2 - α) = -cos α
• cos(3π/2 - α) = -sen α
• tg(3π/2 - α) = 1/tg α

Quando precisares de simplificar expressões trigonométricas complexas, usa estas relações para reduzir os ângulos ao 1º quadrante. Por exemplo:

cos(3π/2 - μ) + 3sen(π - μ) - tg(π + μ) × cos(-μ) = -sen μ + 3sen μ - tg μ × cos μ = 2sen μ - sen μ = sen μ

💡 Estas fórmulas de redução permitem transformar qualquer expressão trigonométrica numa mais simples. Pratica-as regularmente para ganhares velocidade na resolução de exercícios!

Equações Trigonométricas

As equações trigonométricas são resolvidas encontrando todos os ângulos que satisfazem uma condição. Conhece as soluções básicas:

• sen α = 0 ⟹ α = kπ, k ∈ ℤ (0°, 180°, 360°...)
• sen α = 1 ⟹ α = π/2 + k2π, k ∈ ℤ (90°, 450°...)
• sen α = -1 ⟹ α = -π/2 + k2π, k ∈ ℤ (270°, 630°...)

Para resolver equações mais complexas, isola a função trigonométrica:

• sen$2x-π$ + 2 = 2 ⟹ sen$2x-π$ = 0 ⟹ 2x-π = kπ ⟹ x = $π + kπ$/2

Quando tens produtos ou expressões com funções quadráticas:

• sen²x - sen x = 0 ⟹ sen x$sen x - 1$ = 0
• Solução 1: sen x = 0 ⟹ x = kπ
• Solução 2: sen x = 1 ⟹ x = π/2 + k2π

💡 Numa equação do tipo sen α = sen β, lembra-te que há duas possibilidades: α = β + k2π ou α = π - β + k2π. Esta segunda possibilidade é frequentemente esquecida!

Equações Trigonométricas (Continuação)

Quando resolves equações trigonométricas, segue estas regras:

Para equações do tipo sen u = sen α:

• u = α + k2π ou u = π - α + k2π, k ∈ ℤ

Para equações do tipo cos u = cos α:

• u = α + k2π ou u = -α + k2π, k ∈ ℤ

Exemplo completo: sen$2u - π/3$ = √2/2 ⟹ sen$2u - π/3$ = sen(π/4)

Então:

• 2u - π/3 = π/4 + k2π ou 2u - π/3 = π - π/4 + k2π
• 2u = 7π/12 + k2π ou 2u = 13π/12 + k2π
• u = 7π/24 + kπ ou u = 13π/24 + kπ

Outras fórmulas importantes:

• cos u = 1 ⟹ u = k2π, k ∈ ℤ
• cos u = -1 ⟹ u = π + k2π, k ∈ ℤ
• cos u = 0 ⟹ u = π/2 + kπ, k ∈ ℤ

💡 Lembra-te sempre de verificar se as tuas soluções fazem sentido dentro do domínio indicado no problema. Às vezes, nem todas as soluções são válidas no intervalo pedido!

Função Seno

A função seno f(x) = sen x tem as seguintes características:

• Domínio: ℝ (todos os números reais)
• Contradomínio: [-1, 1]
• Zeros: x = kπ, k ∈ ℤ
• Sinal:
  • Positivo no 1º e 2º quadrantes: ]k2π, $k+1$π[
  • Negativo no 3º e 4º quadrantes: ]$k+1$π, $k+2$π[

A função seno é:

• Crescente nos intervalos $k2π, π/2 + k2π$ e $3π/2 + k2π, 2π + k2π$
• Decrescente nos intervalos $π/2 + k2π, 3π/2 + k2π$

Pontos notáveis:

• Máximos: 1 quando x = π/2 + k2π
• Mínimos: -1 quando x = 3π/2 + k2π
• Período: 2π

💡 A função seno é ímpar, o que significa que sen$-x$ = -sen(x). Isto cria uma simetria em relação à origem do gráfico, facilitando o seu esboço.